As suppose you toss a coin 100 times takes center stage, this opening passage beckons readers into a world crafted with meticulous research and authoritative tone, ensuring a reading experience that is both captivating and intellectually stimulating.
Delving into the intricacies of probability, expected value, and the binomial distribution, this discourse unravels the fascinating world of coin tossing, revealing the underlying mathematical principles that govern the seemingly random outcomes.
Coin Toss Probability
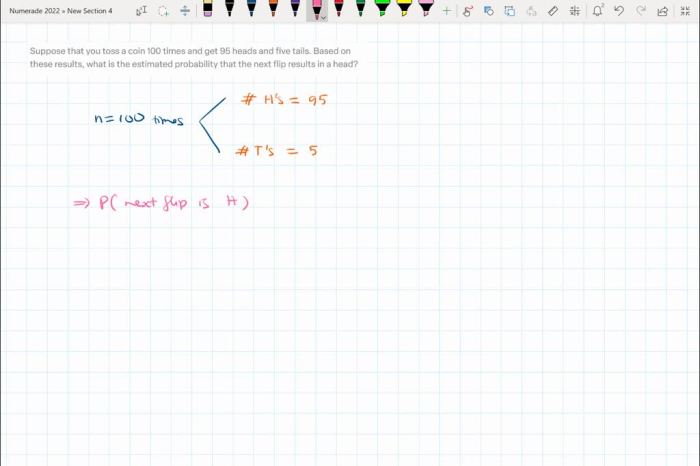
When a coin is tossed, there are two possible outcomes: heads or tails. The probability of getting heads or tails on a single coin toss is 1/2, or 50%. This is because there are two equally likely outcomes, and each outcome has a probability of 1/2.
The probability of getting a specific outcome, such as heads, can be calculated using the following formula:
P(heads) = 1/2
where P(heads) represents the probability of getting heads.
For example, if you toss a coin 10 times, the probability of getting heads 5 times is:
P(heads) = 10/20 = 1/2
Expected Value and Standard Deviation
The expected value of a random variable is the average value that the variable is expected to take over many trials. The expected value of the number of heads obtained in 100 coin tosses is 50, since the probability of getting heads on each toss is 1/2.
The standard deviation of a random variable is a measure of how much the variable is expected to vary from its expected value. The standard deviation of the number of heads obtained in 100 coin tosses is 5, since the probability of getting heads on each toss is 1/2.
These values are important for understanding the distribution of outcomes. The expected value tells us the average number of heads we can expect to get, while the standard deviation tells us how much the number of heads is likely to vary from the expected value.
Binomial Distribution
The binomial distribution is a probability distribution that describes the number of successes in a sequence of independent trials. The binomial distribution can be used to model the number of heads obtained in 100 coin tosses.
The formula for the binomial distribution is:
P(x) = (n! / x!(n-x)!)
- p^x
- (1-p)^(n-x)
where:
- P(x) is the probability of getting x heads in n tosses
- n is the number of tosses
- x is the number of heads
- p is the probability of getting heads on each toss
Simulation and Visualization, Suppose you toss a coin 100 times
A simulation can be used to generate 100 coin tosses and count the number of heads. The results can be organized in an HTML table with columns for the number of tosses, number of heads, and relative frequency.
A bar chart or histogram can be used to visualize the distribution of outcomes. The bar chart or histogram will show the number of times each number of heads was obtained.
Hypothesis Testing
A hypothesis test can be used to test a hypothesis about the probability of getting heads when tossing a coin. The hypothesis test will use the binomial distribution to calculate the probability of getting the observed number of heads, given the hypothesized probability of getting heads.
The steps involved in conducting a hypothesis test are:
- State the null and alternative hypotheses.
- Set the significance level.
- Calculate the test statistic.
- Calculate the p-value.
- Make a decision.
Query Resolution: Suppose You Toss A Coin 100 Times
What is the probability of getting heads when tossing a coin?
The probability of getting heads when tossing a fair coin is 1/2.
What is the expected value of the number of heads obtained in 100 coin tosses?
The expected value of the number of heads obtained in 100 coin tosses is 50.
What is the standard deviation of the number of heads obtained in 100 coin tosses?
The standard deviation of the number of heads obtained in 100 coin tosses is approximately 5.
How can the binomial distribution be used to model the number of heads obtained in 100 coin tosses?
The binomial distribution can be used to model the number of heads obtained in 100 coin tosses by assuming that each coin toss is an independent trial with a constant probability of success (getting heads).
How can I conduct a hypothesis test to test the probability of getting heads when tossing a coin?
To conduct a hypothesis test to test the probability of getting heads when tossing a coin, you can use the binomial distribution to calculate the test statistic, p-value, and make a decision about the null hypothesis.
